Knowledge graph completion task를 계속 진행해 봅시다. 이제는 Multi-hop KG completion이 task로 나왔습니다.
Recap: KG Completion Task
KG completion task는 큰 KG가 주어졌을 때, KG completion를 하는 방법을 찾는 문제입니다. 구체적으로 이야기하면, $(head, relation)$이 주어지고, missing $tail$을 맞추는 task입니다.
여기서는 one-hop query에서 나아가 complex query에 대한 답을 하는 것이 목표입니다. Path query와 conjuctive query가 예시입니다. Path query는 multi-hop query라 볼 수 있고, conjunctive query는 두 query를 and 조건으로 만족하는 query라고 볼 수 있습니다.
Path query는 one-hop query의 연속으로 generalize 가능합니다. $v_a$를 anchor entity라고 하며, query $q$에 대한 답을 $[q]_G$로 표기합니다.
가장 직관적인 path query에 대한 답변 방식은 KG를 모두 훑어보는 것입니다. 하지만 KG에는 필연적으로 빈 연결이 존재합니다. 우리가 기존에 사용중인 약물 중에서 COVID-19을 치료하는 약물이 이미 나왔을 수도 있습니다. 다만 우리가 모르고 있을 뿐입니다. 이런 빈 연결들 때문에 무작정 traverse(훑어보는)하는 것은 효율이 낮습니다.
정리하면, KG는 incomplete하고, 그 어떤 상태에서도 complete 하다고 단정할 수 없습니다. Missing relation, missing entity이 매우 많습니다. 따라서 모든 entity에 대한 답을 traversing 하면서 얻는 것은 불가능 합니다.
그렇다면 KG completion을 전부 수행한 이후에 traverse하면 괜찮을까요? 그렇지 않습니다. KG는 dense한 graph로 모든 연결성을 확인할 수는 없습니다. Time complexity가 $O(d^L_{max})$이기 때문에, 이는 매우 infeasible한 대안입니다. 우리는 incomplete한 KG에서도 predictive query에 대한 답을 하기 위해 missing information을 즉각적(implicitly)으로 imputation해야만 합니다.
Answering Predictive Queries on Knowledge Graphs
Answering에서 가장 중요한 아이디어는 query를 embedding space로 mapping하고, 그 space상에서 reasoning을 하는 것입니다.
Query $\mathbf{q} = \mathbf{h} + \mathbf{r}$ 라고 표현할 수 있습니다. 이때 answer embedding은 $\mathbf{t}$이고, $(\mathbf{q}, \mathbf{t})$ 사이의 거리를 최소화해야 합니다. TransE의 아이디어와 동일합니다.
이런 형태로 answering 문제를 풀게 되면, 단순 addition으로 path query를 해결할 수 있습니다. TransR, DistMult, ComplEx는 composition relation을 표현하지 못하여 path query에 적합하지 않습니다.
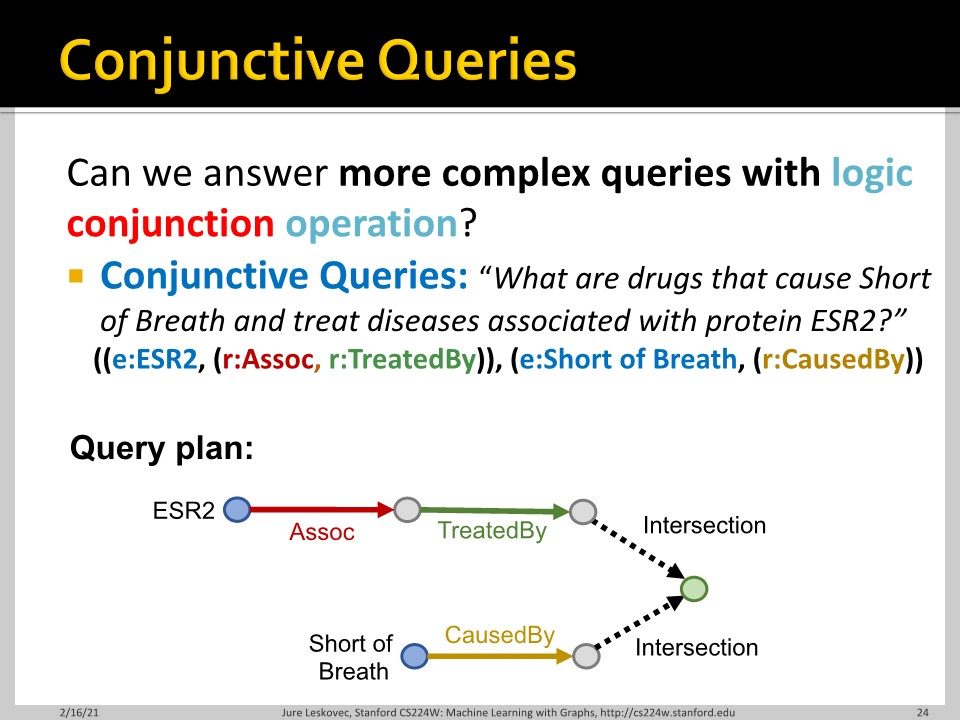
그렇다면 conjunctive query에는 어떻게 답할 수 있을까요? 이때는 두 node에서 출발한 두 relation에 대한 답을 구해야만 합니다.
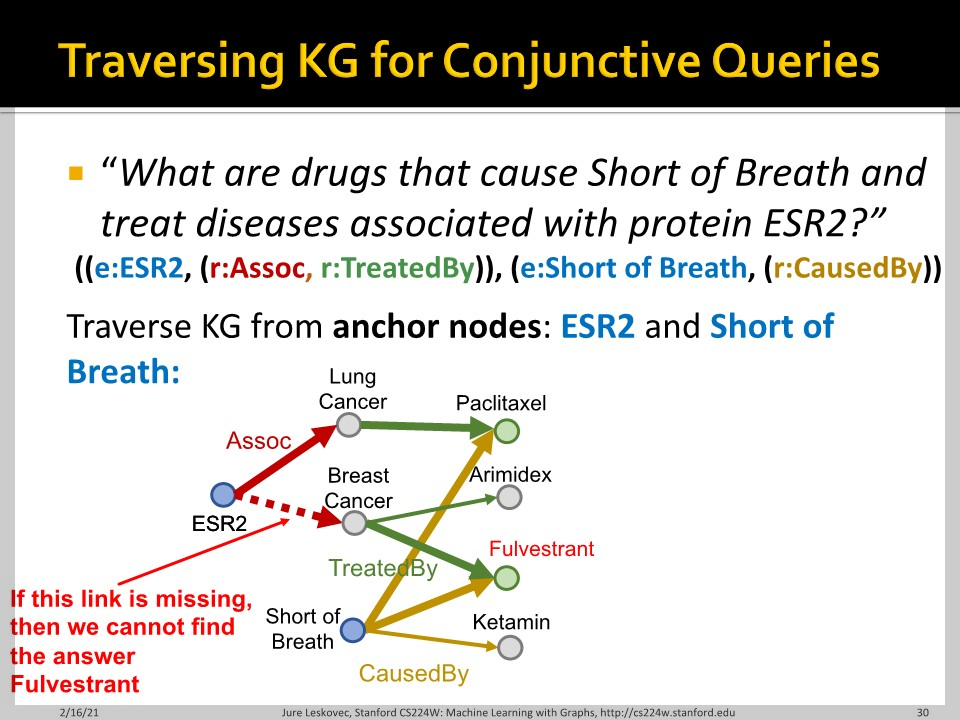
Traverse method로 답을 구할수도 있겠지만, 만약 특정 link가 missing이라면 traverse의 결과는 정상적인 답은 아닐 것입니다. 이를 극복하기 위해서는 implicit하게 관계를 impute 해야합니다. KG에서는 edge 하나가 missing이어도 주변 node들로 유추해서 impute할 수 있는 경우가 있습니다. ESR2가 상호작용하는 다른 protein들을 활용해서 관계를 구할 수 있지 않을까요? 서로 연결된 node의 set을 어떻게 표현할 수 있고, intersection을 latent space에서 어떻게 표현할 수 있을까요? 해당 내용은 part 2에서 이어집니다.
