그래프 generation은 지금까지 다룬 graph 문제와는 또 다른 형태의 problem formulation 입니다.
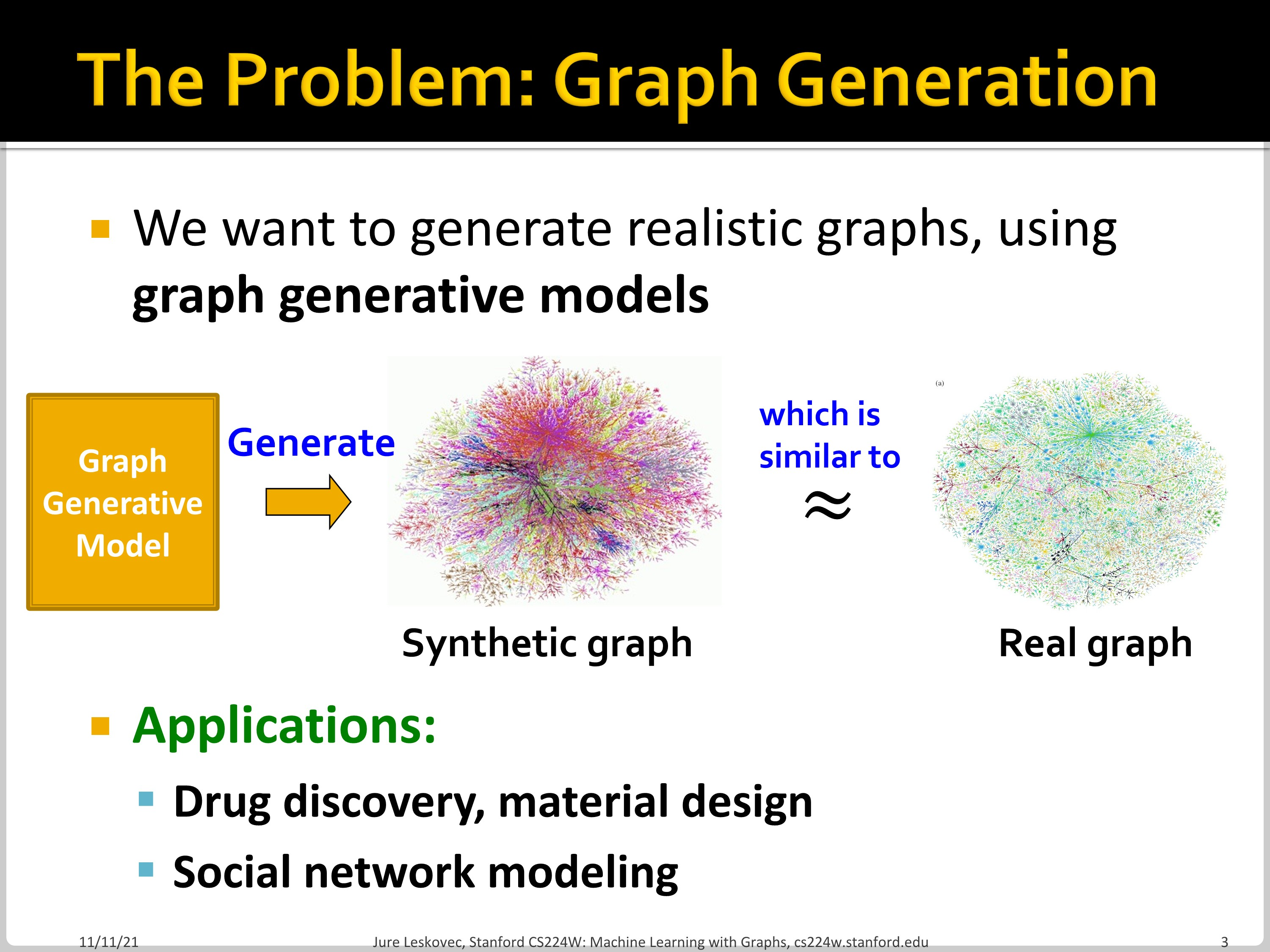
Synthetic graph를 만드는 방법에 대해서 이야기하는 chapter입니다. Graph generation은 drug discovery, social network modeling 등에 적용할 수 있습니다. 다른 활용 범위로는 아래의 예시들이 있습니다.
Graph generation을 학습하는 이유
- Insights: graph formulation/structure에 대한 insight 획득
- Predictions: graph의 미래 변형에 대한 예측
- Simulations: graph instance에 대해 simulation. (요즘 3D simulation에 graph가 많이 쓰입니다.)
- Anomaly detection: graph가 normal/abnormal 인지 결정하는 데에 사용
Graph generation는 아래와 같은 과정으로 발전하였습니다.
- Real-world graph의 특성을 이해하는 task
- 전통적인 graph generative models 구축
- Deep graph generative models
이번 chapter에서 다룰 부분은 deep graph generation model입니다. 지금까지 우리가 graph를 embedding으로 encoding 하는 작업을 했다면, 이제 embedding에서 graph를 generate하는 decoding 문제를 풀어야 합니다.
Machine Learning for Graph Generation
Graph generation tasks는 크게 두 가지로 나뉩니다.
- Task 1: Realistic graph generation
- 주어진 graph data와 유사한 형태의 graph를 생성하는 task.
- 이번 lecture 15에서 주로 다루는 내용
- Task 2: Goal-directed graph generation
- 어떤 objective나 constraint를 만족하는 graph를 생성하는 task
- 어떤 물성을 가지도록 약물을 generation

Graph generative modeld은 기본적으로 MLE (maximum likelihood estimation)입니다.
Graph Generation 문제의 setup과 goal은 아래와 같습니다.
- Setup
- $p_{data}(x)$: data distribution
- 알려지지 않았고, 알 수도 없음
- $x_i \sim p_{data}(x)$ 에서 sampling 된 $x_i$ 활용
- $p_{model}(x;\theta)$: model
- Model is parametrized by $\theta$
- $p_{data}(x)$를 approximate 하는 데 사용
- $p_{data}(x)$: data distribution
- Goal
- Density estimation
- $p_{model}(x;\theta)$를 $p_{data}(x)$에 비슷해지도록 만듦
- Sampling
- $p_{model}(x;\theta)$에서 sampling하여 graph를 생성
- Density estimation
Generative model은 두 가지 방법으로 생성됩니다.
- Density estimation
- Key principle: Maximum Likelihood
- $\theta^* = argmax_\theta \mathbb{E}{x \sim p{data}} \log p_{model}(x | \theta)$
- 즉, data $x$를 만들어 냈을 것 같은 model을 찾는 것이 목적입니다.
- Sampling
- 어떤 complex distribution에서 graph sampling을 하는 단계
- Simple noise distribution에서 sampling
- $z_i \sim N(0,1)$
- 어떤 함수 $f(\cdot)$에 의해 noise를 transform하는 단계
- $x_i = f(z_i;\theta)$
- 이때 $f$는 deep neural network를 사용해 학습
- 어떤 complex distribution에서 graph sampling을 하는 단계

Auto-regressive model에서 $p_{model}(x;\theta)$는 density estimation과 sampling 모두에 사용됩니다. Chain rule에 의해, joint distribution은 conditional distribution의 product입니다.
$p_{model}(x;\theta) = \prod^n_{t=1}p_{model}(x_t | x_1, ..., x_{t-1};\theta)$
$x_t$는 node를 추가하고, edge를 추가하는 $t$번째 action 입니다.
GraphRNN: Generating Realistic Graphs
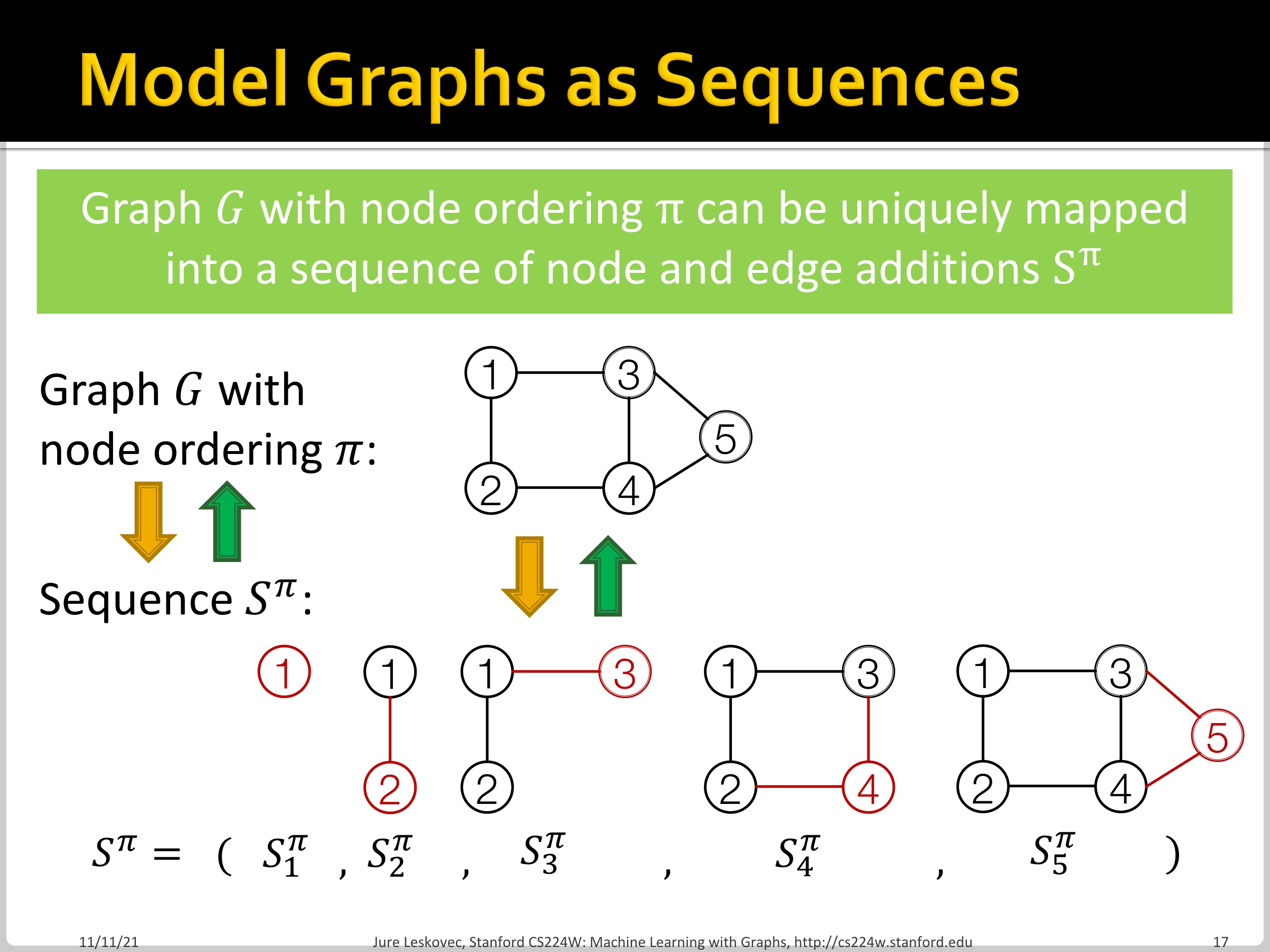
GraphRNN에서는 node와 edge를 순차적으로 추가하면서 graph를 generate합니다. Graph를 sequence로 modeling하여 two level approach를 시행합니다. Node/Edge-level RNN으로 나누는 것인데요, Node-level RNN이 edge-level RNN을 위한 initial state를 만들어 줍니다. Edge-level RNN은 순차적으로 새로운 node가 다른 이전의 node들과 연결될지 안 될지를 예측합니다.
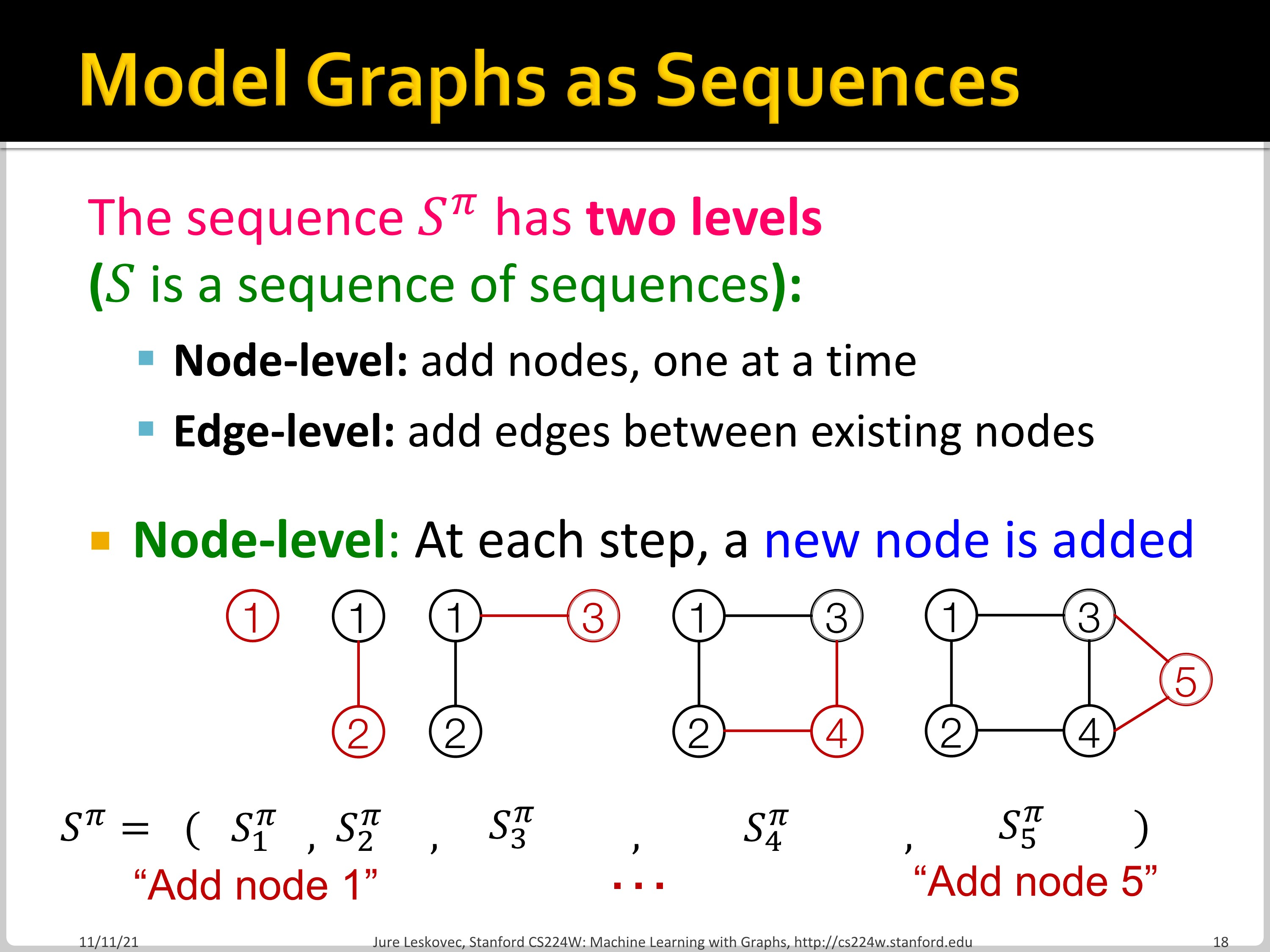
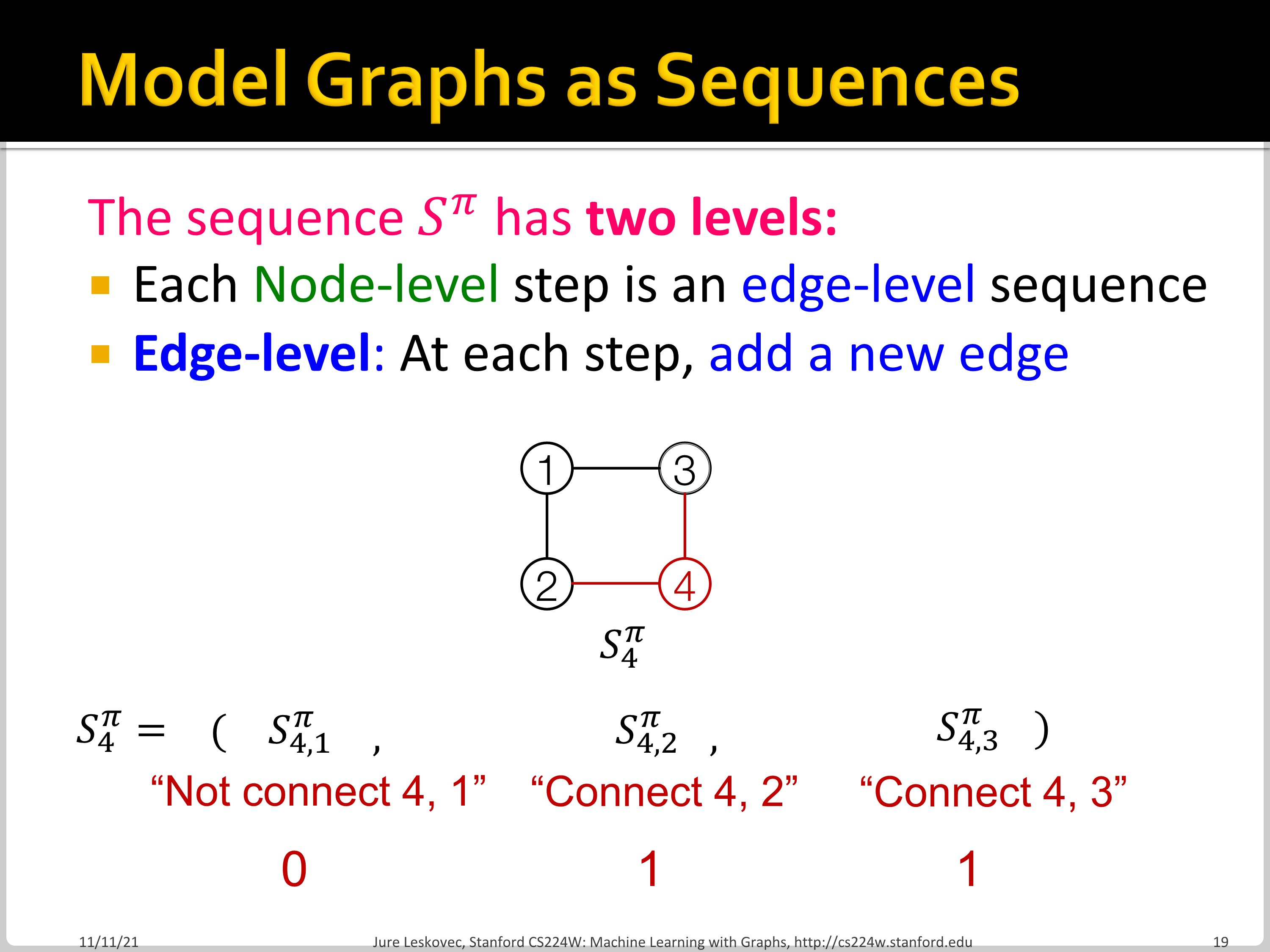
위처럼 Node-level RNN은 node를 추가하고, Edge-level RNN은 edge를 추가합니다.
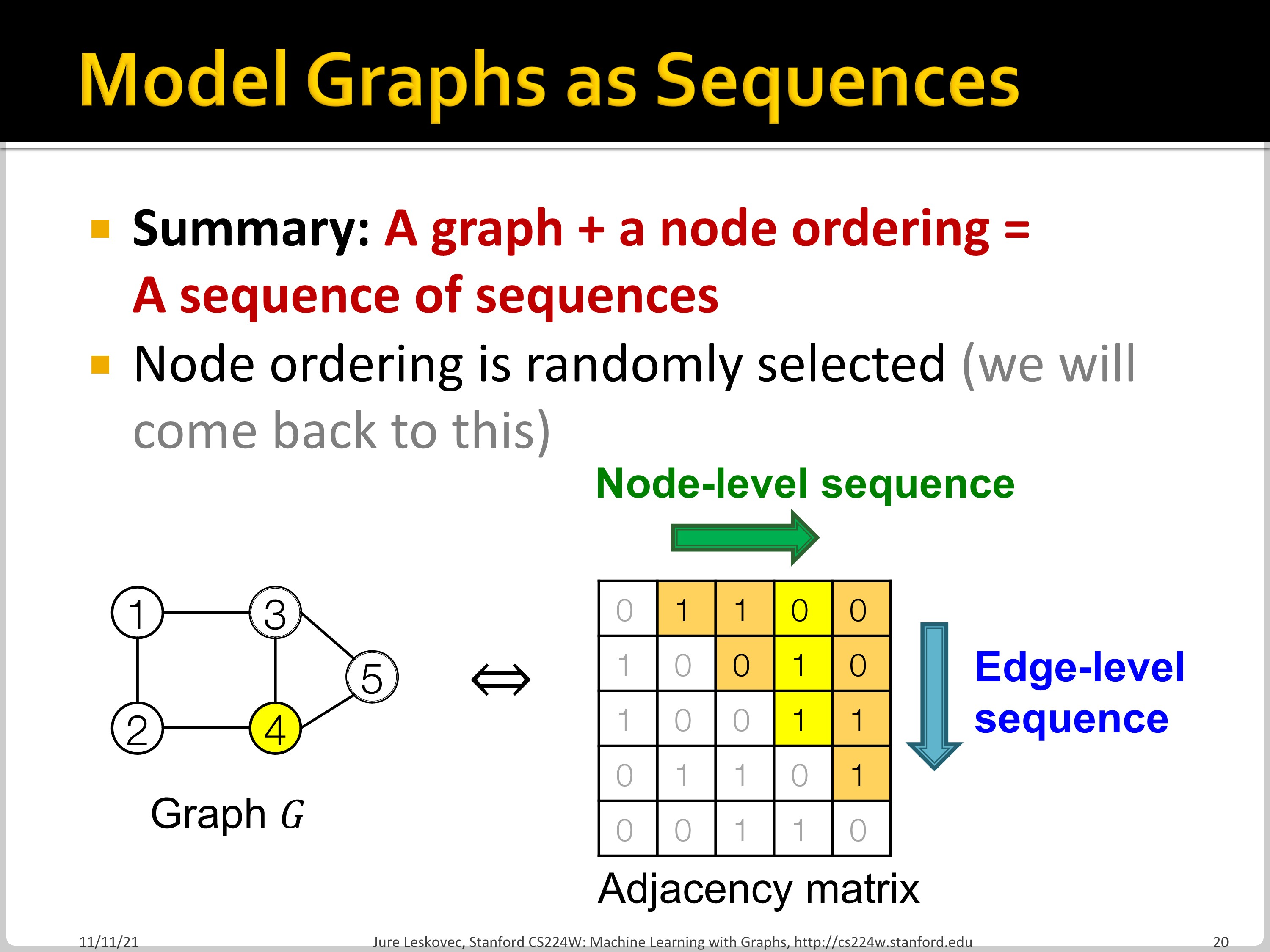
위 matrix에서 행 방향은 Node-level sequence, 열 방향을 Edge-level sequence임을 알 수 있습니다.
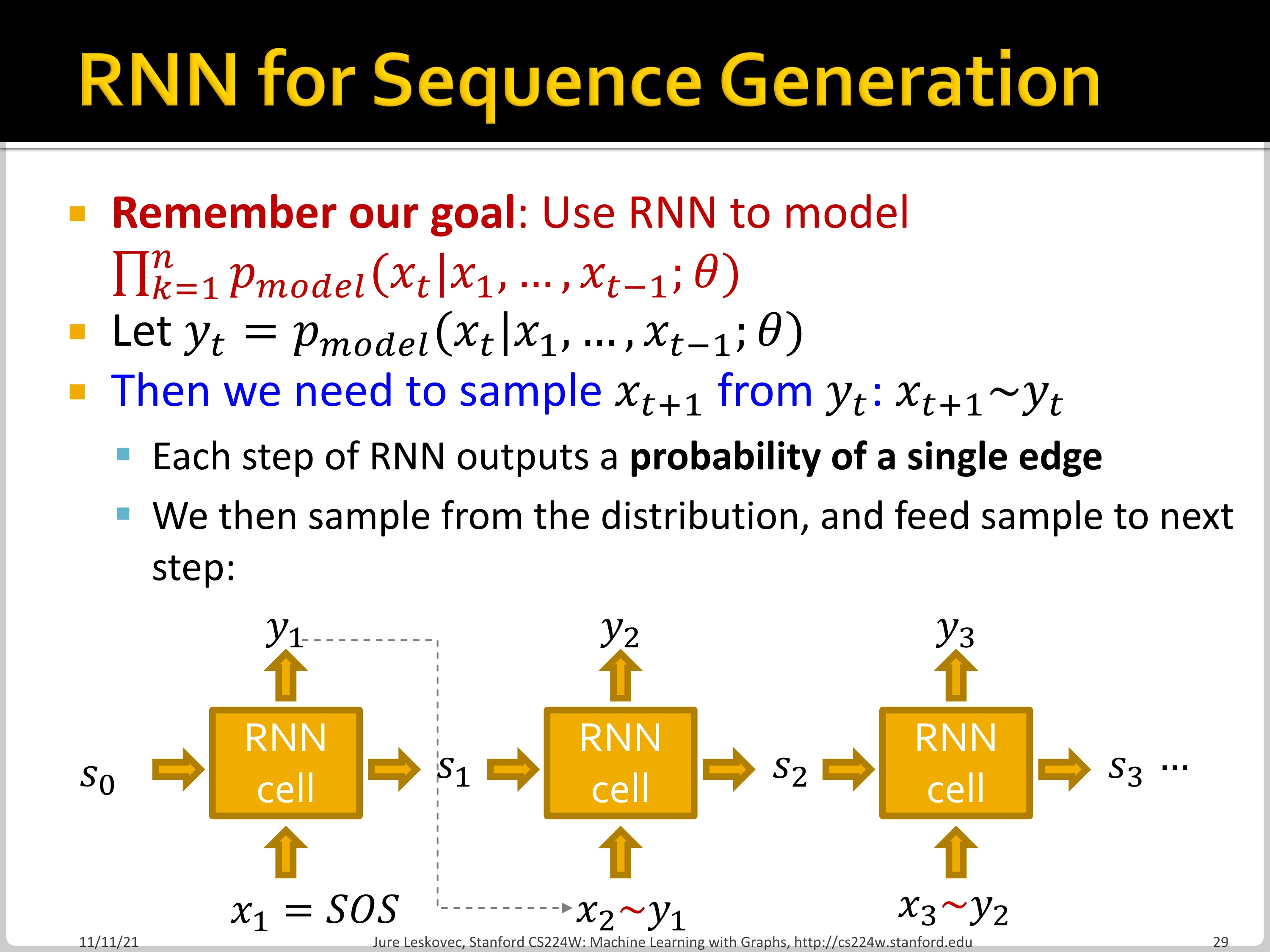
Graph generation을 RNN sequence로 보면, 이전 cell의 output을 다음 cell의 input으로 사용하여 graph를 generate할 수 있습니다. 하지만 이 방법은 deterministic합니다.
우리의 목표는 $\prod^n_{k=1}p_{model}(x_t|x_1, ..., x_{t-1};\theta)$를 modeling 하는 것이므로, 따라서, $x_{t+1}$을 $y_t$에서 sampling 해서 사용할 수 있습니다.

Time step $t$에서 $y_t$를 예측하고, Bernoulli distribution에 따라 $x_{t+1}$을 $y_t$에서 sampling 된 0 또는 1로 부여합니다. 그 0 혹은 1의 값을 그다음 cell의 input으로 사용합니다. 이때 학습 시에는 teacher forcing을 활용합니다. 전 단계에서 틀린 값을 예측해도 맞는 값을 넣어주면 됩니다. Loss는 node/edge의 유무에 따라 binary cross entropy를 활용합니다.

지금까지의 내용을 정리하면 위처럼 됩니다.
'Machine Learning > CS224W' 카테고리의 다른 글
| CS224w - 16. Advanced Topics in Graph Neural Networks Part 1 (0) | 2022.12.04 |
|---|---|
| CS224w - 15. Deep Generative Models for Graphs Part 2 (0) | 2022.11.30 |
| CS224w - 14. Community Detection in Networks Part 2 (0) | 2022.11.21 |
| CS224w - 14. Community Detection in Networks Part 1 (0) | 2022.11.21 |
| CS224w - 13. GNNs for Recommender Systems Part 2 (0) | 2022.11.21 |



