MinCutPool: 이론편1 (MinCutPool: Understanding the Theory 1)

MinCutPool은 복잡한 그래프에서 주요한 node를 추출하고자 한 여러 시도들 중 하나입니다. 일반적으로 node 추출은 graph를 matrix로 표현한 뒤 고유값 분해를 통해 핵심 node를 결정하는 spectral clustering(SC) 방법을 활용합니다. 하지만 고유값 분해 과정의 계산 복잡도가 높아 ( $O(N^3)$ ) scalability issue가 있습니다. 최근 gradient descent 알고리즘을 활용하여 복잡도를 $O(N^2)$ 이나 $O(N)$ 까지 줄이는 연구가 있었습니다(Han & Filippone, 2017). 인공신경망을 이용한 연구도 진행되어 Autoencoder를 활용해 Laplacian matrix(Degree matrix - Adjacency matrix)의 i번째 행을 주요한 eigenvector들의 i번째 component에 연결시키는 작업도 이루어졌습니다(Tian et al., 2014). (Laplacian matrix에 대한 설명은 이 링크를 클릭하세요.)

본 논문에서는 eigenvector를 활용해야 하는 SC의 단점을 해소하면서 graph topology와 node의 feature를 기반으로 node를 clustering하는 방법론을 제시합니다. 이제부터 이론에 대해서 알아봅시다.

$\begin{aligned} \bar{\mathbf{X}} &= \mathrm{GNN}(\mathbf{X},\tilde{\mathbf{A}};\mathbf{\Theta_{\mathrm{GNN}}}) \\ \mathbf{S} &= \mathrm{softmax}(\mathrm{MLP}(\bar{\mathbf{X}};\Theta_{\mathrm{MLP}})) \end{aligned}$

$\bar{\mathbf{X}}$ 는 MP(Message passing, 하나의 graph neural layer 층으로 생각하면 됨)들을 통과하여 얻어진 node representation matrix입니다. $\bar{\mathbf{X}}$ 를 multi-layer perceptron(MLP, basic한 인공 신경망)과 softmax에 연달아 통과시켜 cluster assignment matrix ${\mathbf{S}}$ 를 얻습니다. 이때 $\Theta_{\mathrm{GNN}}$ 와 $\Theta_{\mathrm{MLP}}$ 는 훈련 가능한 파라미터입니다. $\mathbf{S}$ 는 $[N \times K]$ 행렬으로 i번째 행에 node i가 각 cluster에 속할 확률을 담고 있습니다. $\mathbf{S}$ 가 softmax를 통과하는 과정에서 $\mathbf{S}$ 의 원소 $\mathbf{S}_{ij}$ 는 $\mathbf{s}_{ij}\in [0,1]$ 를 만족합니다. 그리고 $\mathbf{S}\mathbf{1}_K=\mathbf{1}_N$ 가 성립하게됩니다. ( $[N \times K] \times [K \times 1]=[N \times 1]$ , N개의 node, K개의 cluster)

그래프의 예시와 함께 확인해보겠습니다. 아래는 9개의 node로 이루어진 그래프와 그 인접행렬입니다.

이 그래프의 최적 클러스터가 각각 적색, 녹색, 청색이라고 가정해봅시다. 그러면 최적 cluster 구성을 담은 행렬 $\mathbf{C}$ 를 표기할 수 있습니다. 그리고 $\mathbf{C}\mathbf{1}_K=\mathbf{1}_N$ 가 됨을 보일 수 있습니다.

최적 cluster(정답)가 아닌 예측 결과 행렬 $\mathbf{S}$ 에서도 $\mathbf{S}\mathbf{1}_K=\mathbf{1}_N$ 는 성립합니다. $\mathbf{S}$ 의 i 번째 행은 i 번째 node가 각 cluster에 속할 확률을 나타냅니다.

행렬 $\mathbf{S}$ 는 MinCutPool의 loss에 중요하게 작용합니다. MinCutPool은 두 가지 loss로 이루어져 있습니다. 첫 번째는 cut loss $\mathcal{L}_c$ , 두 번째는 orthogonality loss $\mathcal{L}_o$ 입니다. $\mathcal{L}_c$ 에 대해서 먼저 확인해보겠습니다.

$\begin{aligned} \mathcal{L}_c = - \frac{\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{A} \mathbf{S})} {\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{D} \mathbf{S})} \end{aligned}$

$\mathcal{L}_c$ 는 'cluster 내부의 연결성/graph 전체의 연결성'으로, cluster 내부가 전체적인 graph의 연결성과 비교해서 얼마나 끈끈히 연결되어 있는지 알려줍니다. $\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{A} \mathbf{S})$ 이 cluster 내부의 연결성, $\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{D} \mathbf{S})$ 가 graph 전체의 연결성을 나타냅니다. $\mathbf{D}$ 는 $\mathbf{A}$ 의 degree matrix입니다. 예시 code와 함께 살펴봅시다.

import numpy as np
c = [[1, 0, 0],
     [1, 0, 0],
     [1, 0, 0],
     [0, 1, 0],
     [0, 1, 0],
     [0, 1, 0],
     [0, 0, 1],
     [0, 0, 1],
     [0, 0, 1]]

s = [[0.8, 0.2, 0.0],
     [0.8, 0.2, 0.0],
     [0.8, 0.2, 0.0],
     [0.2, 0.6, 0.2],
     [0.2, 0.6, 0.2],
     [0.2, 0.6, 0.2],
     [0.0, 0.1, 0.9],
     [0.0, 0.1, 0.9],
     [0.0, 0.1, 0.9]]

A = [[0 ,1, 1, 0, 0, 0, 0, 0, 0],
     [1 ,0, 1, 0, 0, 0, 0, 0, 0],
     [1 ,1, 0, 0, 0, 1, 0, 0, 1],
     [0 ,0, 0, 0, 1, 1, 0, 0, 0],
     [0 ,0, 0, 1, 0, 1, 0, 0, 0],
     [0 ,0, 1, 1, 1, 0, 0, 0, 1],
     [0 ,0, 0, 0, 0, 0, 0, 1, 1],
     [0 ,0, 0, 0, 0, 0, 1, 0, 1],
     [0 ,0, 1, 0, 0, 1, 1, 1, 0]]

print(np.transpose(c) @ A)
'''
array([[2, 2, 2, 0, 0, 1, 0, 0, 1],
       [0, 0, 1, 2, 2, 2, 0, 0, 1],
       [0, 0, 1, 0, 0, 1, 2, 2, 2]])
- i번째 행, j 번째 열의 원소는 i 번째 cluster와 j 번째 node 사이의 edge 수를 나타냅니다.
- 조금 다르게 생각하면, cluster들이 자신들의 지분이 있는 edge를 챙겨간다고 볼 수도 있습니다.
'''

print(np.transpose(c) @ A @ c)
'''
array([[6, 1, 1],
       [1, 6, 1],
       [1, 1, 6]])
- i번째 행, j 번째 열의 원소는 i 번째 cluster와 j 번째 cluster 사이의 edge 수를 나타냅니다.
- 또 조금 다르게 생각하면 np.transpose(c) @ A에서 챙긴 node별 edge 중, 진짜 자신의 cluster와 
  연결된 edge만을 가져갑니다.
'''

print(np.transpose(s) @ A)
'''
array([[1.6, 1.6, 1.8, 0.4, 0.4, 1.2, 0. , 0. , 1. ],
       [0.4, 0.4, 1.1, 1.2, 1.2, 1.5, 0.2, 0.2, 1. ],
       [0. , 0. , 0.9, 0. , 0. , 0.9, 1.8, 1.8, 1.8]])
- 여섯째 열(node 6)을 기준으로 생각하면, node 6에 연결된 edge 4개를 clsuter red에 1.2개,
  cluster green에 1.5개, cluster blue에 0.9개 분배했습니다.
- node 6에 edge를 제공하던 node는 3, 4, 5, 9번 입니다.
- 그리고 node 3, 4, 5, 9의 cluster별 지분대로 np.transpose(s) @ A 여섯째 열의 원소가 결정됩니다.
'''

print(np.transpose(s) @ A @ s)
'''
array([[4.4 , 2.3 , 0.9 ],
       [2.3 , 2.86, 1.26],
       [0.9 , 1.26, 4.86]])
- np.transpose(c) @ A @ c와 마찬가지로 i번째 행, j번째 열의 원소는 i번째 cluster가
  j번째 cluster와 연결된 edge의 숫자를 나타냅니다.
'''

print(np.trace(np.transpose(s) @ A @ s))
'''
- 따라서 trace를 구하게 되면 i번째 cluster 내부의 edge 수의 합을 구할 수 있습니다.
'''

곱해지는 matrix가 adjacency matrix가 아닌 degree matrix가 되면 오히려 더 간단해집니다. Cluster 별로 edge를 분배하던 것을 넘어, 이제 모든 edge의 sum을 구하게 됩니다.

D = np.diag(np.sum(A, axis=1) # Degree matrix를 생성합니다.

print(np.transpose(s) @ D @ s)
'''
array([[5.44, 2.24, 0.32],
       [2.24, 3.28, 1.68],
       [0.32, 1.68, 6.8 ]])
- 정확한 원리까지는 모르겠지만, np.transpose(s) @ A @ s 보다 조금 더
  전체적인 연결성을 대변하는 듯 합니다.
'''

그렇다면 1번 node의 가중치에 따라서 $-\frac{\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{A} \mathbf{S})} {\mathrm{Tr}(\mathbf{S}^{\top} \mathbf{D} \mathbf{S})}$ 의 값은 어떻게 변화할까요? 정답에 해당하는 [1.0, 0.0, 0.0]부터 [0.0, 1.0, 0.0] 까지 첫 두 개의 원소 값만 조절하면서 비교해보았습니다.

import numpy as np
import matplotlib.pyplot as plt

s = [[0.9, 0.1, 0.0],
     [0.8, 0.2, 0.0],
     [0.8, 0.2, 0.0],
     [0.2, 0.6, 0.2],
     [0.2, 0.6, 0.2],
     [0.2, 0.6, 0.2],
     [0.0, 0.1, 0.9],
     [0.0, 0.1, 0.9],
     [0.0, 0.1, 0.9]]


A = [[0 ,1, 1, 0, 0, 0, 0, 0, 0],
     [1 ,0, 1, 0, 0, 0, 0, 0, 0],
     [1 ,1, 0, 0, 0, 1, 0, 0, 1],
     [0 ,0, 0, 0, 1, 1, 0, 0, 0],
     [0 ,0, 0, 1, 0, 1, 0, 0, 0],
     [0 ,0, 1, 1, 1, 0, 0, 0, 1],
     [0 ,0, 0, 0, 0, 0, 0, 1, 1],
     [0 ,0, 0, 0, 0, 0, 1, 0, 1],
     [0 ,0, 1, 0, 0, 1, 1, 1, 0]]

D = np.diag(np.sum(A, axis=1))

a11 = np.arange(1.0, -1e-5, -0.01)
a12 = np.arange(0.00, 1.0+1e-5, 0.01)
a13 = np.zeros(len(a11))
a1 = np.stack((a11, a12, a13), 1)

result = []
min = 0
min_idx = 0

for i, a in enumerate(a1):
  s[0] = a
  result.append(-np.trace(np.transpose(s) @ A @ s)/np.trace(np.transpose(s) @ D @ s))
  if min>result[i]:
    min = result[i]
    min_idx = i

print(min, a1[min_idx])
'''
-0.8204945376760294 [0.87 0.13 0.  ]
'''
plt.scatter(a11, result)
plt.xlabel('Value of s11')
plt.ylabel('loss')
plt.show()

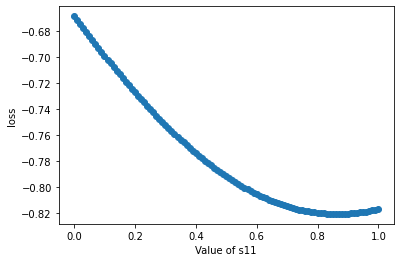
처음에는 loss가 s11의 값이 [1.00, 0.00, 0.00]일 때 최소일 줄 알았는데 꼭 그렇지는 않습니다. 같은 cluster에 속한 다른 node들의 clusterg assignment 값인 [0.80, 0.20, 0.00]과 [1.00, 0.00, 0.00]의 가중 평균 즈음에 해당하는 [0.87 0.13 0.00]에서 최소치를 보입니다. 알다가도 모르겠지만, 정답 cluster에 제대로 접근하는 것과, 같은 cluster내 node 사이의 균형성을 모두 고려하는 듯 합니다. 혹은 3번 node가 node 1, 2와 연결되어 있으니, 실제로 일부 지분은 cluster 2와 cluster 3에 해당할지도 모릅니다. 논문에서 서술한 cut loss의 특성은 다음과 같습니다.

$\mathcal{L}_c$ 는 강하게 연결되어 있는 node가 서로 함께 cluster 되도록 한다고 합니다. $\mathcal{L}_c$ 의 최대값은 0으로, graph 내에 연결된 node가 모두 다른 cluster에 속할 때 최대값에 도달합니다. 최소값은 1로, cluster끼리의 연결이 없으면서 한 cluster내의 node들은 모두 동일하며 다른 cluster와 orthogonal한 $\mathbf{S}$ 를 가질 때 발생합니다. $\mathcal{L}_c$ 는 non-convex한 문제여서 local minima에 갇힐 우려가 있다고 합니다. 예를 들어 모든 node를 한 cluster로 묶거나, 모든 node가 모든 cluster에 균일하게 퍼지는 경우입니다.

s = [[1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3],
     [1/3, 1/3, 1/3]]

print(-np.trace(np.transpose(s) @ A @ s)/np.trace(np.transpose(s) @ D @ s))
'''
-1
'''

s = [[1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0],
     [1.0, 0.0, 0.0]]

print(-np.trace(np.transpose(s) @ A @ s)/np.trace(np.transpose(s) @ D @ s))
'''
-1
'''

MP operation 자체가 node feature를 uniform하게 하는 경향이 있어 이런 local minima에 갇힐 위험이 더욱 올라갑니다. 이럴 때를 대비해서 orthogonality loss가 존재합니다. 이 orthogonality loss에 대한 자세한 정보는 다음 글에서 확인해보도록 하겠습니다.

출처

Bianchi, Filippo Maria, Daniele Grattarola, and Cesare Alippi. "Spectral clustering with graph neural networks for graph pooling." In International Conference on Machine Learning, pp. 874-883. PMLR, 2020.
Han, Yufei, and Maurizio Filippone. "Mini-batch spectral clustering." In 2017 International Joint Conference on Neural Networks (IJCNN), pp. 3888-3895. IEEE, 2017.
Tian, Fei, Bin Gao, Qing Cui, Enhong Chen, and Tie-Yan Liu. "Learning deep representations for graph clustering." In Proceedings of the AAAI Conference on Artificial Intelligence, vol. 28, no. 1. 2014.

저작자표시 비영리 동일조건

'Machine Learning' 카테고리의 다른 글

Type of Attention (어텐션의 종류) (0)	2022.12.27
Bagging, Boosting, Bootstrapping, Stacking (0)	2022.02.12
MinCutPool: 코드 분석 (MinCutPool: Understanding the Code) (0)	2022.02.12
MinCutPool: 이론편2 (MinCutPool: Understanding the Theory 2) (0)	2022.02.12
Einsum 입문하기 (Introduction to Einsum) (0)	2022.01.25

내 블로그 - 관리자 홈 전환	`Q` `Q`
새 글 쓰기	`W` `W`

글 수정 (권한 있는 경우)	`E` `E`
댓글 영역으로 이동	`C` `C`

이 페이지의 URL 복사	`S` `S`
맨 위로 이동	`T` `T`
티스토리 홈 이동	`H` `H`
단축키 안내	`Shift` + `/` `⇧` + `/`

Archive: 그냥 적기

MinCutPool: 이론편1 (MinCutPool: Understanding the Theory 1)

출처

'Machine Learning' 카테고리의 다른 글

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역

MinCutPool: 이론편1 (MinCutPool: Understanding the Theory 1)

출처

'Machine Learning' 카테고리의 다른 글

관련글

티스토리툴바

단축키

내 블로그

블로그 게시글

모든 영역