두 번째 graph neural network(GNN)을 활용한 시계열 예측 논문입니다. 제목은 Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting입니다.
Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting
- 2019년 7월 17일 publish
- In Proceedings of the AAAI conference on artificial intelligence
- Shengnan Guo, Youfang Lin, Ning Feng, Chao Song, and Huaiyu Wan
- 2022년 8월 7일 기준 citation 수 692회
북경 교통대학교 연구진들의 연구 내용입니다. 주안점 및 과거 연구의 한계, 활용 데이터 및 기타 설정, 인접 행렬 설계, 모델 설계 사항, 모델 내 데이터 차원, 모델 설계 특이점, 결과 및 분석, 결과 특이 사항, 교통 공학적 분석 내용, 결과 특이사항, 의문점 및 느낀점 순으로 정리해보겠습니다.
주안점 및 과거 연구의 한계
- 기존 연구들읜 동적인 traffic data의 spatio-temporal 한 특징을 파악할 수 없음
- Input이 2D/3D 그리드에 그치는 경우가 많음,
- Recent, daily-periodic, weekly-periodic 종속성을 반영하기 위해 세 종속 파트를 결합함
- 각 종속 파트는 spatio-temporal 어텐션 메커니즘과 sptio-temporal convolution(graph convolution) 파트로 구성됨
- Attention based Spatial-Temporal Graph Convolution Network (ASTGCN)를 제시함
- Spatial attention과 temporal attention을 각각 적용하였고, 각 attention을 위한 convolution module을 제작
- 특히 spatial attention을 위해서는 graph convolution을 활용함
활용 데이터 및 기타 설정
- PeMSD4 (California Department of Transportation에서 취득): 3848개 수집점(29개 도로), 30초 단위 원시 데이터를 5분 단위로 집계, 속력/교통량/점유율 데이터, 2018년 1월~2월, 첫 50일이 training set, 나머지가 test set
- PeMSD8 (California Department of Transportation에서 취득): 1979개 수집점(8개 도로), 30초 단위 원시 데이터를 5분 단위로 집계, 속력/교통량/점유율 데이터, 2016년 7월~8월, 첫 50일이 training set, 나머지가 test set
- 수집점 사이의 간격이 3.5miles이상이 되게 하기 위해서 그보다 작은 거리에 있는 센서는 제외시켰음. PeMSD4에는 307개, PeMSD8에는 170개 데이터 포인트만 남음
- 없는 데이터는 linear ineterpolation
- Zero-mean normalization (x′=x−mean(x))
인접 행렬 설계
- 설명 없음. 보통 이런 경우는 거리 반비례로 많이 함
모델 설계 사항
- Recent segment, daily-periodic segment, weekly-periodic segment로 구성됨

- 6월 14일의 오전 8:00~8:55의 교통 정보를 예측한다고 하고, 예측 시간의 2배에 해당하는 데이터를 사용한다고 가정. Th는 그 직전 2시간, Td는 같은 시간대의 2일 전 데이터, Tw는 같은 시간, 요일의 2주 전까지의 데이터 사용. 참고로 아래 그림의 Tw에 6월 17일은 오타로 보이며, 실제로는 6월 7일을 표기하고 싶었던 듯

- Residual learning framework 적용함. 대부분의 논문들이 residual learning을 사용하는 것으로 보임
- 같은 시간 축에서는 graph convolution, 시간 축으로 전개하는 과정에서는 같은 node끼리 convolution함

- 행렬곱 및 더하기 연산으로 서로 다른 시간 단위에서 얻어진 feature들을 fusion하였음

- 제안하는 ASTGCN에서 spatial-temporal attention을 제거하여 낮은 성능을 나타내는 Multi-Component Spatial-Temporal Graph Convolution Networks (MSTGCN)를 같이 비교하였음
모델 내 데이터 차원
- G=(V,E,A)
- |V|=N, A∈RN×N
- F = length of time series, C = length of feature number, τ = length of time slice
- xc,it∈R, xit∈RF, Xt=(x1t,x2t,...,xNt)∈RN×F
- χ=(X1,X2,...,Xτ)T∈RN×F×τ
- Traffic flow of node i at time t in the future yit=xf,it∈R
- Future traffic flow sequences Y=(y1,y2,...,yN)T∈RN×Tp
- Future traffic flow of node i from τ+1 yi=(yiτ+1,yiτ+2,...,yiτ+Tp)∈RTp
- The recent segment χh=(Xt0−Th+1,Xt0−Th+2,...,Xt0)∈RN×F×Th
- 최종 input 차원은 RN×F×Tx, 여기서 x는 h, d, w 중 하나로 prediction 목표인 Tp의 정수배
- Spatial attention 부분에서 χ(r−1)h rth spatial-temporal block의 input일 때
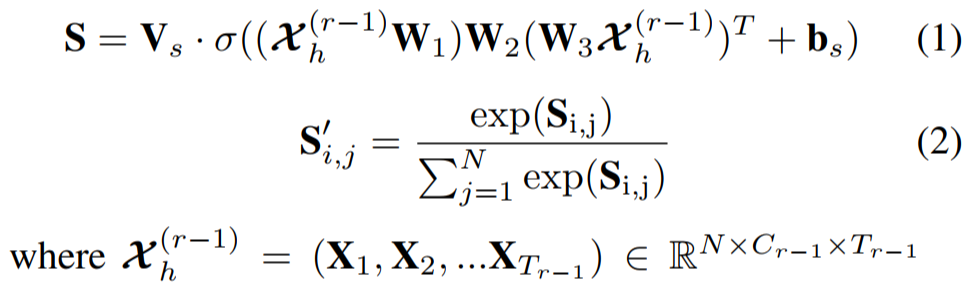
- Vs,bs∈RN×N, W1∈RTr−1, W2∈RCr−1×Tr−1, W3∈RCr−1
- Spatial attention matrix S′∈RN×N
- Temporal attention 부분은 아래와 같음
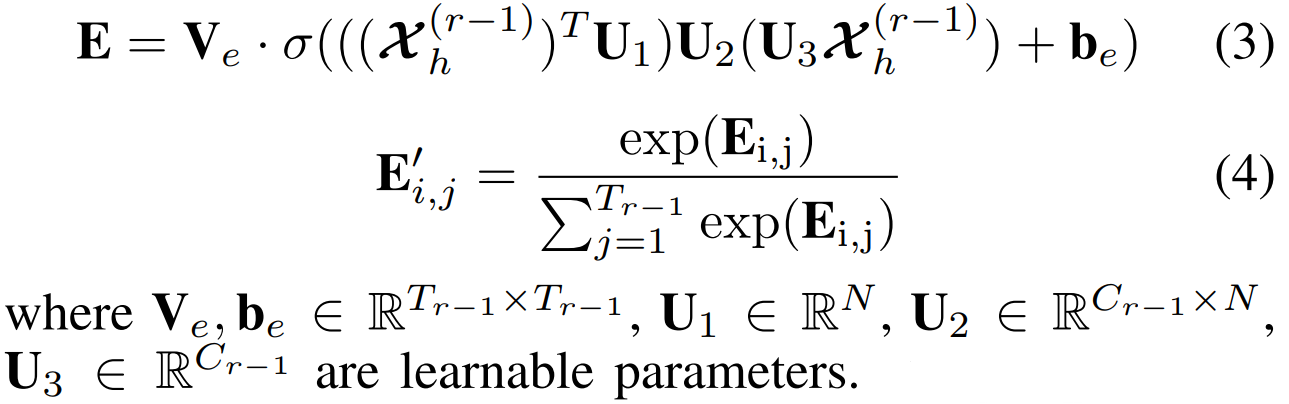
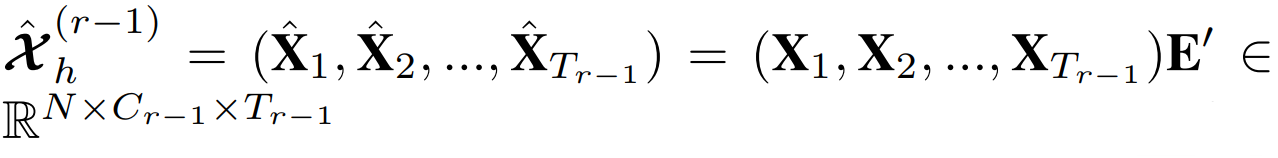
- 시간 차원 맞추어서 데이터가 나오게 spatial attention과 temporal attention을 설계하였음
모델 설계 특이점
- 같은 time step에서는 그래프 내부의 convolution, 다른 timestep 끼리는 temporal convolution 진행. 이제는 일반적인 approach라고 봐야 할듯
결과 및 분석
- MSTGCN, ASTGCN 모두 나아진 성능을 보였음. 다만 어떤 식으로 측정하였는지 확인 필요함.
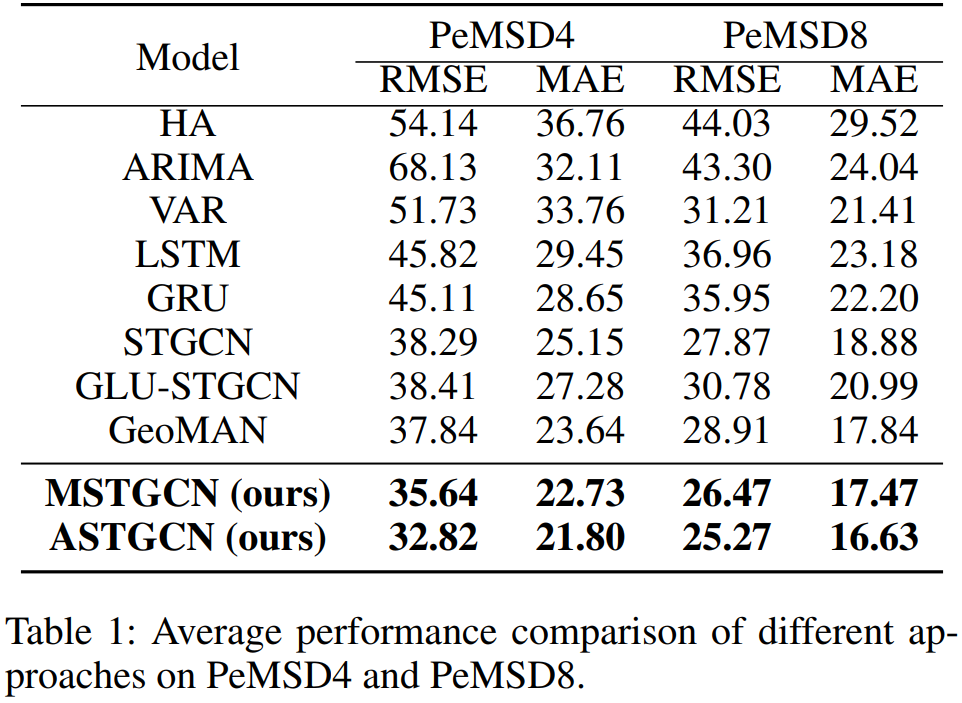
결과 특이 사항
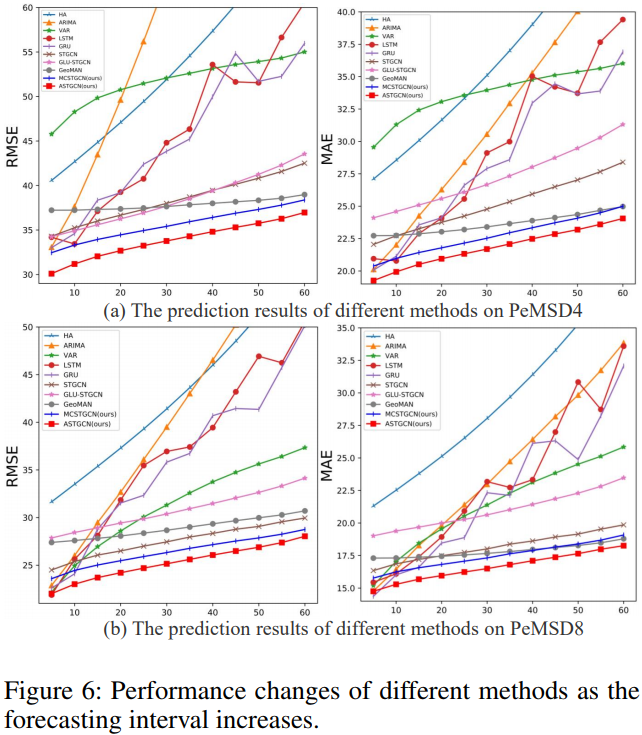
- 예측하고자 하는 시간이 현재 time stamp에서 멀수록 error가 증가함. ASTGCN이 증가분이 작은 것을 확인할 수 있음
- 네트워크의 스케일이 큰 PeMSD4에서 더 큰 에러를 보임
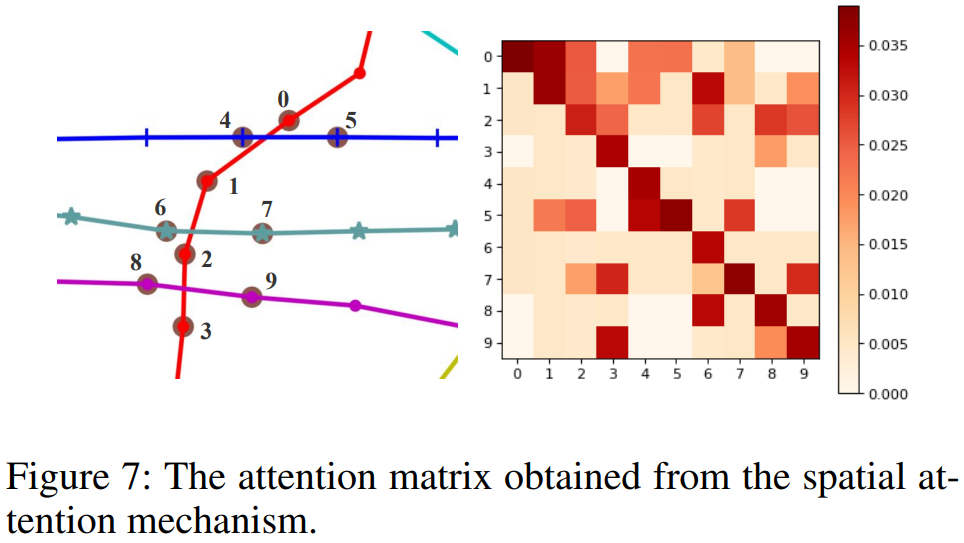
교통 공학적 분석 내용
- 170개 데이터 포인트를 가진 PeMSD8 데이터 중 10개를 골라서 average spatial attention matrix를 시각화 하였음
의문점 및 느낀점
- 시간 차원 맞추어서 데이터가 나오게 spatial attention과 temporal attention을 설계하였는데, 과연 차원만 맞춘다고 그것이 spatial attention 혹은 temporal attention이 되는가? 될 것 같은 생각도 듦. 같은 time stamp 값 사이의 attention을 구한다면, spatial 해질 것이고, 다른 time stamp 값 사이의 attention을 구하면 temporal할 것
- RMSE가 30이 넘어가는데, 그럼 12개 time stamp의 에러를 더한 것인가?
- 위의 Figure 7에서 8번 도로에 대한 attention value가 가장 큰 것이 2, 3, 9번이 아니라 간접적으로 연결되어 있는 6번인데 그 이유는 무엇인가?


