이번 node classification 문제를 주위 node에서 message(feature)를 전달 받는 message passing scheme으로 풀게 됩니다. 몇몇 node는 ground truth가 있어야 message를 전달 받을 수 있습니다. 따라서 일부 node의 label을 안 상태에서 다른 node의 label을 확인하는 semi-supervised node classification 문제로 접근합니다. 일부 node만 알고 있다면 어떻게 접근할 수 있을까요? 우리는 아래 세 가지 방법을 통해서 위 문제를 해결할 것 입니다.
- Relational classification
- Iterative classification
- Correct & Smooth
비슷한 성질을 지내고 있는 node는 서로 가까울 확률이 높습니다. 이를 homophily라고 합니다. 혹은 가까이 있다보면 node의 성질이 비슷해질 수도 있습니다. 이건 influence라고 합니다.
Relational Classifcation
Relational classifier는 node label을 network를 따라서 propagate 시킵니다. label 되어있지 않은 node는 0.5로 initialize 되어있고, 주위 label을 참조하여 update합니다.

이 슬라이드를 보면 직관적으로 이해가 가능합니다. 5번 node를 update할 때는 4번 node를 update한 이후에 그 update한 값을 활용합니다. 방법은 수렴이 보장되지 않고, feature information을 사용할 수 없다는 단점이 있습니다.
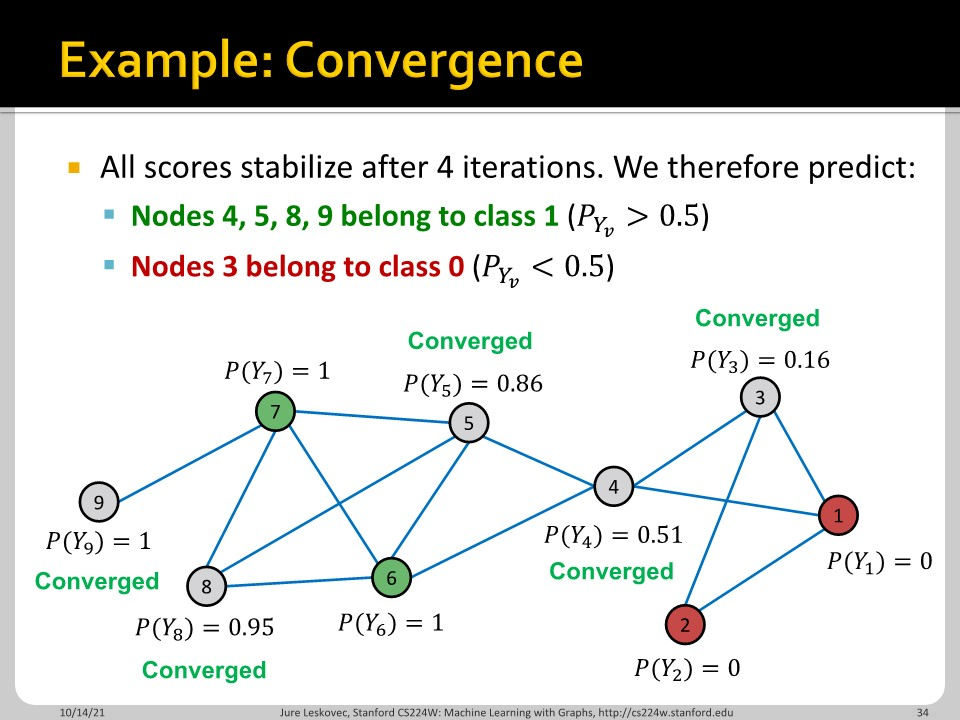
값이 일정 이상으로 변하지 않으면 converge로 판단합니다. 그리고 0.5를 기준으로 label을 진행합니다.
Iterative Classification
Iterative classifier는 node attributes를 활용할 수 있다는 장점이 있습니다. Attributes와 Neighbor set의 label을 활용합니다.

$\Phi_{1}(f_{v})$와 $\Phi_{2}(f_{v}, z_{v})$라는 두 가지 함수를 활용하게 됩니다. $\Phi_{1}(f_{v})$는 base classifier라고 불리며 node feature를 기반으로 node label을 prediction 합니다. $\Phi_{2}(f_{v}, z_{v})$는 relational classifier라고 불리고, node feature vector $f_{v}$와 $v$의 neighbor labels로 이루어진 summary $z_{v}$를 가지고 label prediction을 진행합니다.
$z_{v}$는 여러가지가 가능한데, neighbor label의 histogram일 수도 있고, 가장 common한 label일 수도 있습니다.

Iterative classifier는 두 단계로 나뉘어져 작동합니다.
- 1 단계
- 1. Base classifier : $f_{v}$를 활용하여 $Y_{v}$를 예측
- 2. Relational classifier : $f_{v}$, $z_{v}$를 활용하여 $Y_{v}$를 예측
- 2 단계 (Iterative on test set)
- 1. Base classifier : $f_{v}$를 활용하여 $Y_{v}$를 결정
- 2. Relational classifier : $f_{v}$, $z_{v}$를 활용하여 $Y_{v}$를 예측
- Iterate for each node $v$
- node $u$의 neighbor $N_{v}$로 $z_{v}$ 갱신
- 새로운 $z_{v}$로 $Y_{v}$ 갱신
- 모든 label이 안정되거나 특정 iteration 수에 도달할 때 까지 반복


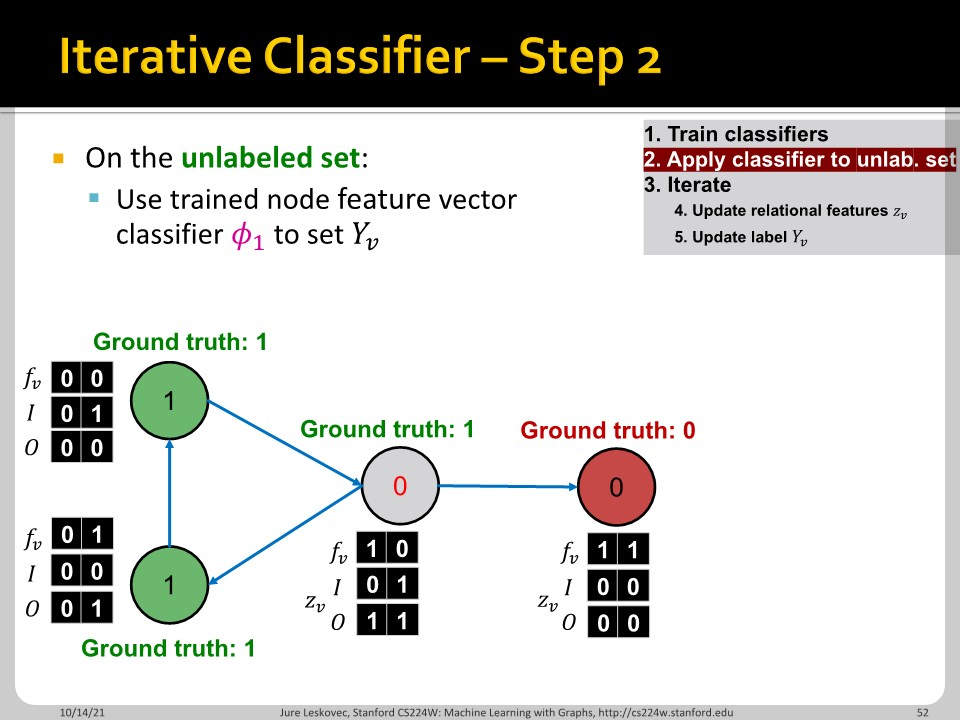



위의 슬라이드들이 과정의 정리된 내용입니다.

이렇게 해서 relational classification과 iterative classification에 대해서 확인해보았습니다.
Collective Classification : Correct & Smooth

Correct & smooth는 마치 teacher network로 만들어진 soft label로 information distilation을 하는 것과 유사합니다. 2021년 10월 OGB leaderboard의 많은 알고리즘들이 correct & smooth를 기반으로 합니다. 위의 과정에서 중요한 것은 3에 해당하는 post-process로 correct step과 smooth step으로 구성됩니다.

먼저 ground-truth label과 soft label의 차이로 training error를 찾습니다. Unlabeled node에 대해서는 진행하지 않습니다.

Edge에 대하여 error를 확산(diffuse) 시킵니다. 이때 $\widetilde{A}=D^{-1/2}(A+I)D^{-1/2}$로, 정규화된 $A$를 의미합니다. ($D$는 $(A+I)$의 degree matrix로 diagonal 성분만 존재합니다.)
이때 $\widetilde{A}$의 모든 eigenvlaue는 [-1, 1] 범위에 포함되며, eigenvalue 1에 대응되는 eigenvector는 $D^{1/2}1$입니다. Eigenvector의 정의에서 출발하면 쉽게 보일 수 있습니다. 또한 $\widetilde{A}$는 거듭제곱에서도 계산이 용이합니다. 그 거듭제곱의 eigenvalue도 [-1, 1] 범위에 놓이며 가장 큰 eigenvalue는 1로 유지된다고 합니다.

Soft label과 Diffused training error의 합이 correct step의 결과물이 됩니다. 이때 scale s는 hyper-parameter가 됩니다.

Smooth step에서는 training label들을 hard label로 대체합니다. 그 다음 다시 한 번 diffusion을 진행합니다. 위 간단한 과정으로 성능이 크게 향상된다고 합니다. 근처에 있는 node들은 비슷한 형태의 error를 가질 것이라고 생각하여 error를 전파한 것이 효과가 있는 것입니다.

이번 장에서는 Relational classification, iterative classification, correct & smooth에 대해서 확인해보았습니다.
'Machine Learning > CS224W' 카테고리의 다른 글
| CS224w - 06. Graph Neural Networks Part 2 (0) | 2022.03.16 |
|---|---|
| CS224w - 06. Graph Neural Networks Part 1 (0) | 2022.03.16 |
| CS224w - 04. Graph as Matrix: PageRank, Random Walks and Embeddings (0) | 2022.03.07 |
| CS224w - 03. Node Embeddings (0) | 2022.02.18 |
| CS224w - 02. Traditional Methods for Machine Learning in Graphs (0) | 2022.02.17 |



