This article summarizes RL Course by David Silver - Lecture 3: Planning by Dynamic Programming. This chapter will discuss policy evaluation, policy iteration, and value iteration. Each concept has an important role in reinforcement learning.
Introduction

Before we start, what is dynamic programming? A dynamic problem has a sequential or temporal component. Programming is optimizing a program(in here, policy). Dynamic programming breaks down the complex problem into subproblems and combines the solution.

We need two requirements for dynamic programming 1. The optimal solution can be decomposed into subproblems. 2. Subproblems recur many times.
The Markov decision process satisfies both properties. Bellman equation itself is a recursive decomposition. The value function is stored and reused over time.

There is two-stage in MDP: prediction and control. In the prediction stage, it predicts the value function given the policy. In the control stage, it controls the policy given the value function.
Iterative Policy Evaluation

An iterative policy evaluation uses Bellman expectation backup to evaluate a given policy π. The process is progressed synchronously. We update whole k+1th state from kth state. It updates vk+1(s) from vk(s′).

The diagram shows how the state value is updated by iterative policy evaluation.

This small grid world is undiscounted. The white room means a non-terminal state. The black room means a terminal state. Each movement has a reward of -1 until the terminal state is reached. After that, the agent follows a uniform random policy.
When the iteration reaches k=2, the greedy policy is updated, and it certainly well behaves than a random policy.

When k=3, an optimal policy is already reached. By iterative policy evaluation with non-optimal policy, we identified an optimal policy.

Given a policy π, when we evaluate the value function with the policy π, greedy action with vπ is an improved policy. In a small grid world example, we reached optimal policy in 3rd iteration, but it usually takes longer than that. This process of policy iteration always converges to π∗.
Policy Iteration
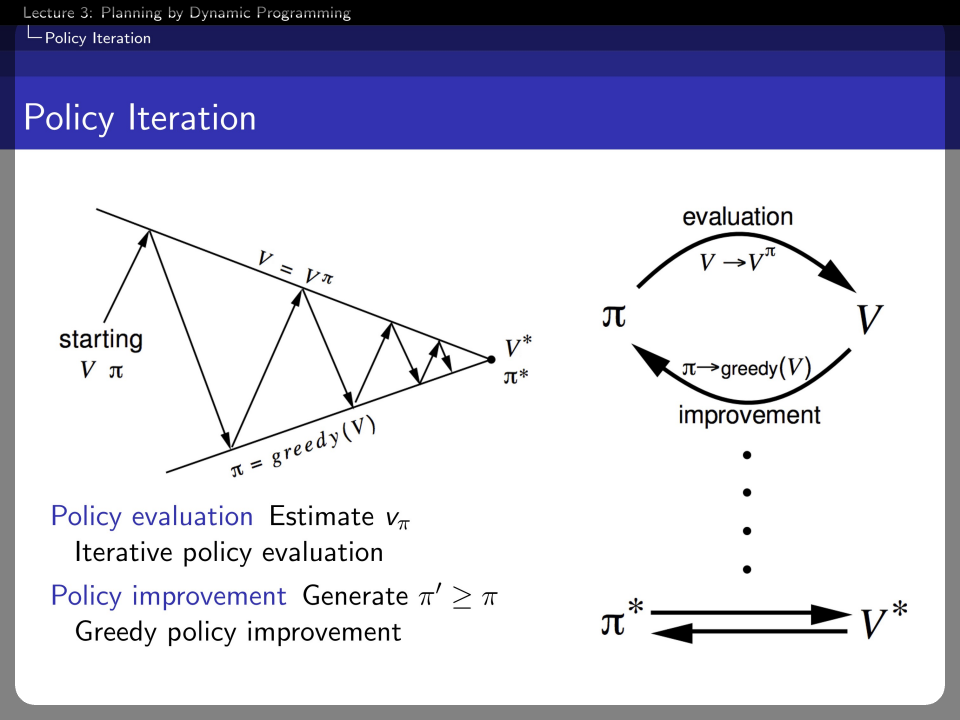
The process we saw in the policy evaluation can be generalized as a policy iteration. Policy iteration repeats the policy evaluation step and policy improvement step.
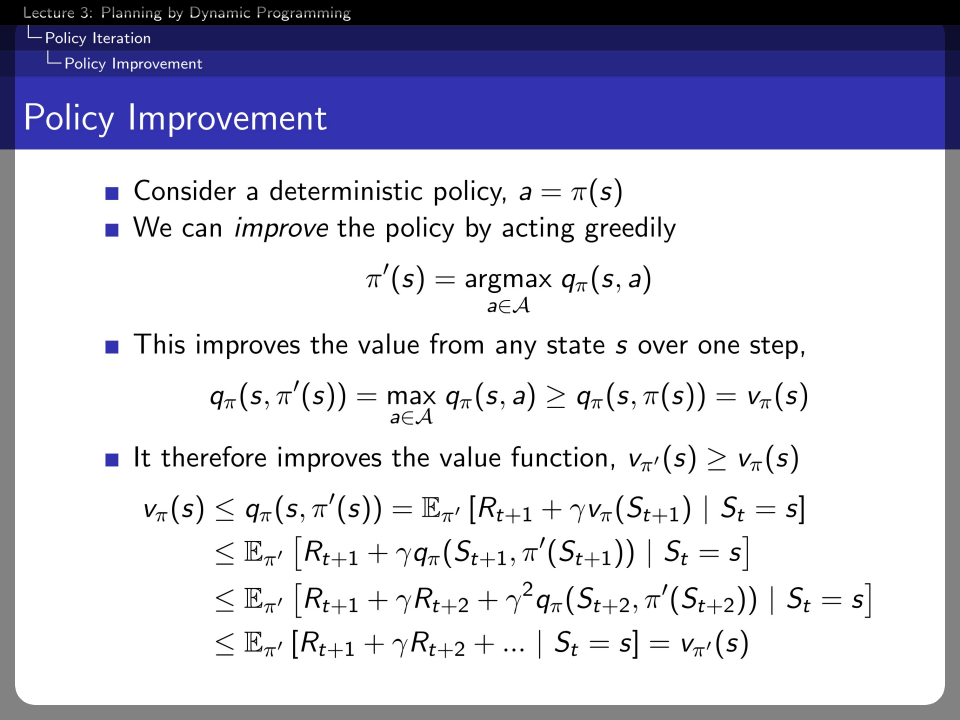
Does acting greedily always give us a better policy? Yes. Because a new policy π′ improves the value from any state s over one step.

If improvements stop, the Bellman optimality equation is satisfied, and therefore vπ(s)=v∗(s) for all s∈S.
In practice, the stopping condition (ϵ-convergence of value function, fixed number of iterations) is discussed.
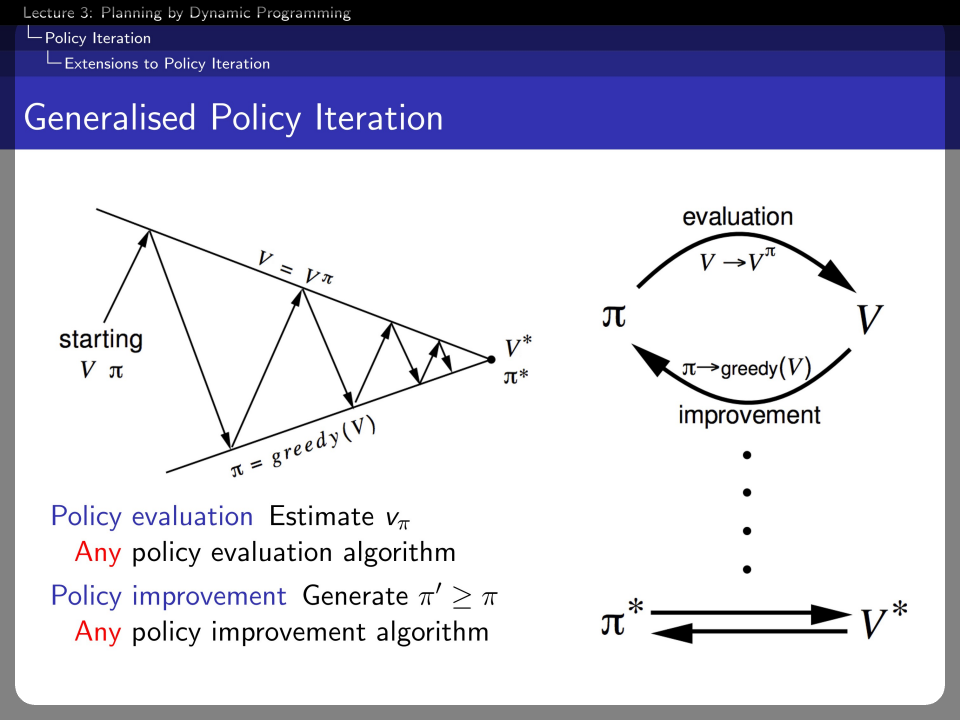
This property can be generalized to any policy. So, reinforcement learning can be applied in various fields.
Value Iteration

We can induce the principle of optimality, which is quite obvious.

If we know the solution to the subproblem, the value of the following state can be found by one-step lookahead. The recursive one-step lookahead becomes a solution for whole states. In value iteration, the lookahead value of a state should give a subsequent state a maximum reward.
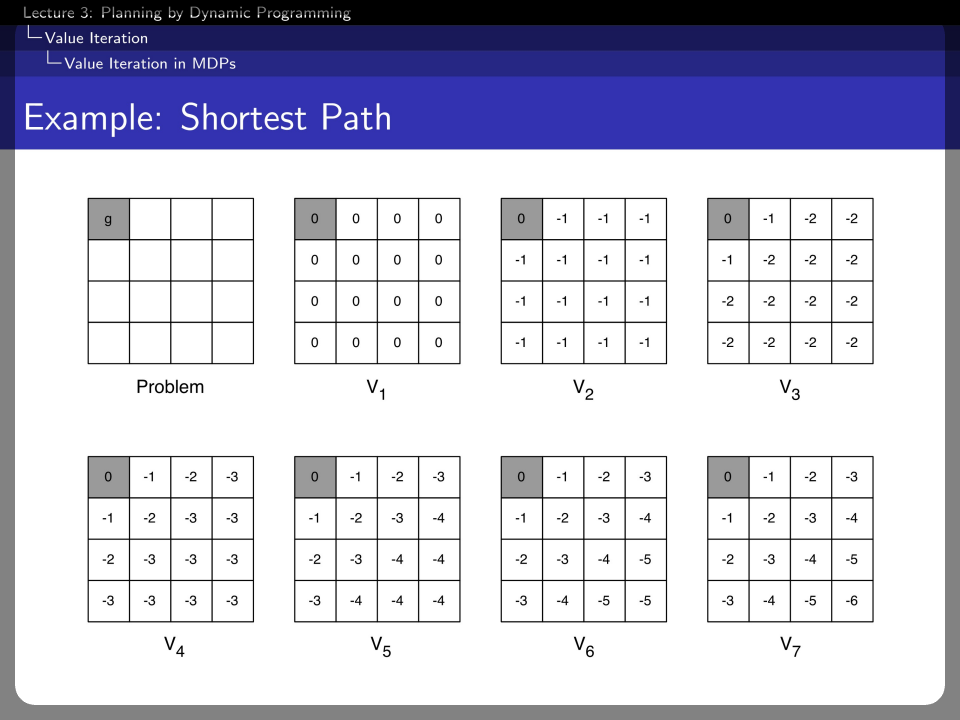
This is the problem of finding the shortest path to goal g. And each state's value is calculated and recursively, from the state near the goal to the state far from the goal.

With a Bellman optimality backup, we can find an optimal value of each state. There is no explicit policy. It just lookup for immediate action, which provides an agent with a greedy update.
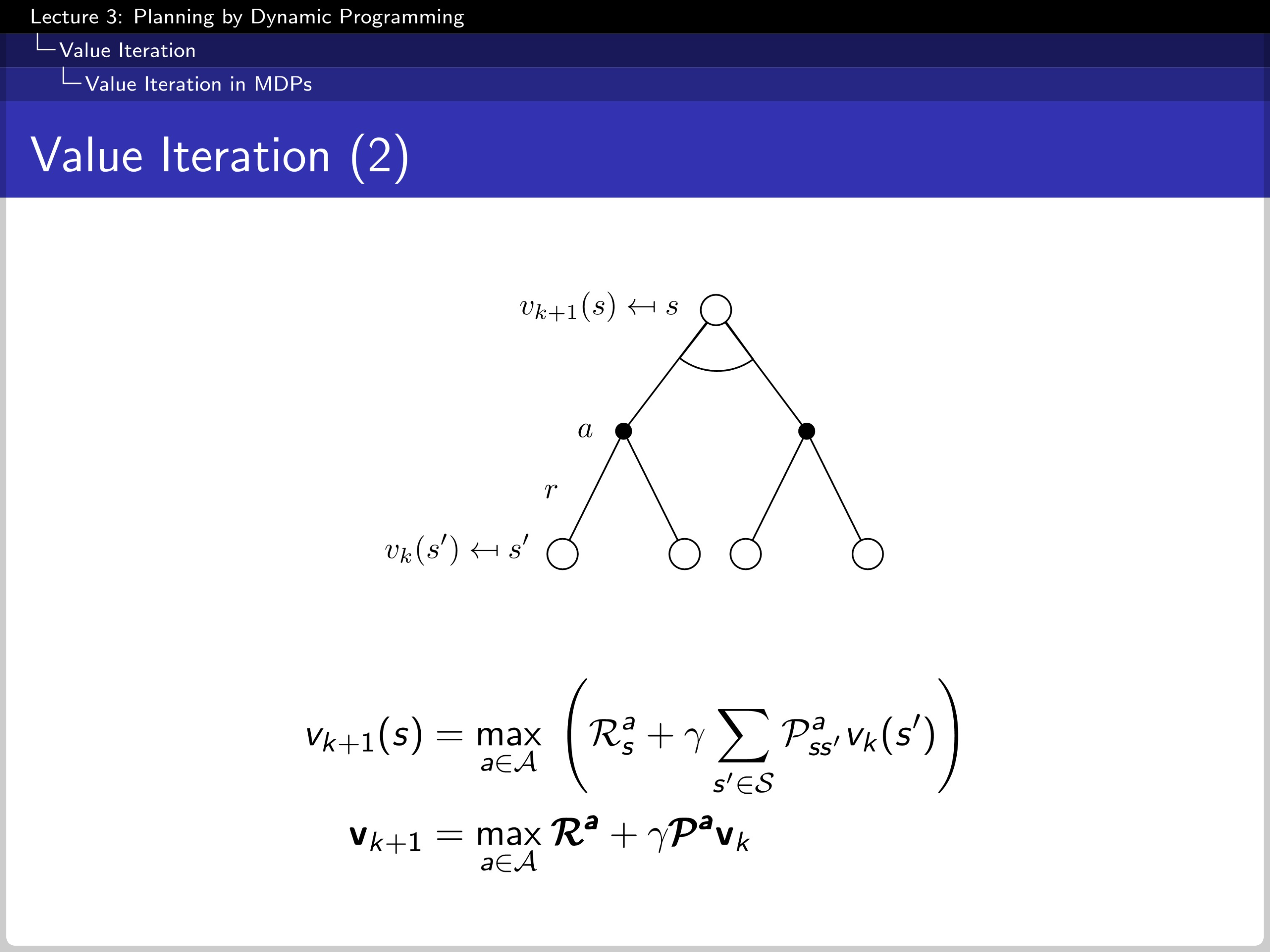
This diagram shows the value iteration process. Where v(k+1) is updated by action from previous sate s′ which gives s a maximum reward.

We can divide the problem into prediction and control. And the algorithm can be divided into iterative policy evaluation, policy iteration, and value iteration. However, acquiring the action-value function requires more complex because it consists of a state-action pair.
'Machine Learning > Reinforcement Learning' 카테고리의 다른 글
| RL Course by David Silver - Lecture 4: Model Free Prediction (0) | 2022.08.04 |
|---|---|
| On-Policy, Off-Policy, Online, Offline 강화학습 (0) | 2022.06.23 |
| RL Course by David Silver - Lecture 2: Markov Decision Processes (0) | 2022.05.03 |
| RL Course by David Silver - Lecture 1: Introduction to Reinforcement Learning (0) | 2022.04.27 |



